

How can we express the intrinsic brightness of a star in terms of magnitudes? One means is to imagine moving the star to a predetermined distance. The absolute magnitude of a star, Mv, is defined to be the apparent brightness of a star when the star is at a distance of 10 pc (32.6 light years). The difference between the apparent magnitude and absolute magnitude provides (almost) enough information to calculate the distance to the star. If you are interested, you can read more about apparent and absolute magnitudes.
In order to find the distance to M100, you need to find the absolute magnitudes for each of the Cepheids. Henrietta Leavitt of the Harvard College Observatory discovered the relationship between the period of Cepheids and their average apparent magnitude mv. She had studied Cepheids in the Large and Small Magellanic Clouds, but did not know the distance to the Cepheids, and therefore could not establish absolute magnitudes or luminosities for the Cepheids. Harlow Shapley determined the calibration needed to turn Leavitt's period - apparent magnitude diagram (P-mv relation) into a period-luminosity relation (P-L relation) for Cepheids. Since the luminosity of a star is related to its absolute visual magnitude (Mv), we can express the P-L relationship as a P-Mv relationship. The P-Mv relationship for M100 is shown graphically below:
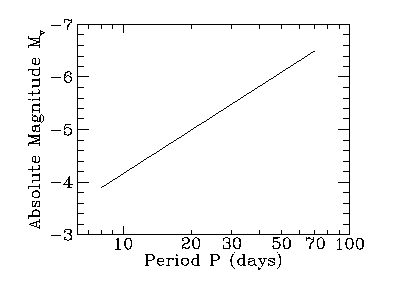
The relationship is described by the equation (from Ferrarese et al., 1996)
where P is in days. If logarithms are a faint memory, you may wish to peruse a refresher on logs.
For each Cepheid you discovered, use the above equation to determine the absolute magnitude of the Cepheid from its period.
For example, in the demonstration of the Cepheid hunt, you found Cepheid C46. Part I, Section B of your lab sheet for this Cepheid looks like this:
Cepheid name Grid # Avg mv P(days) Mv mv-Mv C46 47 25.3 25.3 ____________ ______ ______ _______ ______ ______ ____________ ______ ______ _______ ______ ______From column 4, the period of the Cepheid is 25.3 days. Using the equation above, the average absolute magnitude of C46 is
Enter the absolute magnitude in column 5 of Part I, Section B of your lab sheet. The entry for C46 now looks like:
Cepheid name Grid # Avg mv P(days) Mv mv-Mv C46 47 25.3 25.3 -5.27 ____________ ______ ______ _______ ______ ______ ____________ ______ ______ _______ ______ ______
Find the absolute magnitudes for all your Cepheids, and enter the result in column 5 of Part I, Section B of your lab sheet.
Back to Find the Cepheids!
Back to the table of contents