Estimate the age of the universe!

We can easily estimate the age of the universe if we assume that
the universe has always been expanding at the current rate. Since the
galaxies are currently flying away from each other, we can run the
expansion back in time, and ask how long it would take for all the
galaxies in the universe to come back together again.
First of all, remind yourself of the basic relationship between
velocity, distance and time:
time = distance / velocity.
If we know the distance between M100 and the Milky Way, and their
relative velocity, we can calculate how long it took them to travel
their distance of separation.
age of universe = [ (distance to M100) / (recessional velocity of
M100) ]
In other words,
age = d / v.
Recall that
Ho = v / d,
so the age of the universe is
age = 1 / Ho.
That seems simple enough. There's only one little hitch... We used
units of (km/sec/Mpc) for Ho in the previous
section. Inverting these gives units of (sec Mpc / km) for the age of
the universe. How long is a (sec Mpc / km)?!! We'll have to use
some conversion factors to transform these units into a comprehensible
age.
Using the relationships
- 1 year = 3.15 x 107 sec
- 1 Mpc = 3.09 x 1019 km
we find that
1 sec Mpc (3.09 x 1019 km) (1 year)
Age of universe = ---- ------- ----------------- ----------------
Ho km 1 Mpc (3.15 x 107 sec)
Note that the units of sec, Mpc and km all cancel, leaving an age in
years.
Calculate the age of the universe, using the numerical value for
Ho from Section III. Enter your result in Section
IV, Part A of your lab sheet:
Age of universe = ________________ years. (Constant expansion.)
Does your answer seem reasonable? How does this compare to the
presumed ages of the oldest globular clusters? Write your answer on
your lab sheet in the space provided.
It is unlikely the Hubble constant has been constant over the lifetime
of the universe. The universe has a lot of mass, and gravity tries to
pull all that mass together. Gravity slows the expansion, just as a
ball thrown vertically upwards decelerates from the gravitational pull
of the earth. The age of the universe computed above corresponds to
an "empty universe," one in which the average density of the
universe (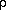 ) is zero. Should the true
age of the universe be larger or smaller than this?
) is zero. Should the true
age of the universe be larger or smaller than this?
The rate at which the expansion has slowed over time depends on the
average density of the universe. The higher the density, the greater
the deceleration. If the density is lower than some critical value we
call 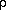 c, the universe will
continue to expand forever. It will get cold and dark. If the
density is higher than
c, the universe will
continue to expand forever. It will get cold and dark. If the
density is higher than 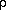 c
the gravitational attraction will eventually halt the expansion, then
begin a contraction toward what has been dubbed the "Big Crunch."
If
c
the gravitational attraction will eventually halt the expansion, then
begin a contraction toward what has been dubbed the "Big Crunch."
If 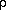 is just equal to
is just equal to 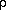 c the expansion will slow to a
stop, but only after an infinite amount of time has passed.
c the expansion will slow to a
stop, but only after an infinite amount of time has passed.
Cosmologists often speak in terms of the density parameter 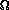 o, defined as
o, defined as
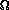 o =
o = 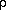 /
/ 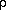 c.
c.
Calculating the density of the universe is no simple task. The
universe contains perhaps ten times more matter than the luminous
matter we can directly detect. We know the "dark matter" is there
because we can see its gravitational effects. Most cosmologists
believe that baryons ("normal matter") comprise at most 10% of all
matter (i.e. 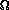 b
b 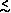 0.1). The other 90% is thought to be composed of
"exotic" particles we cannot easily detect.
0.1). The other 90% is thought to be composed of
"exotic" particles we cannot easily detect.
The age of the universe you calculated above corresponds to the case
when 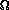 o = 0. Suppose the average
density of the universe is equal to the critical density, so that
o = 0. Suppose the average
density of the universe is equal to the critical density, so that 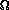 o = 1. In that case, it can be shown that
the age of the universe is given by
o = 1. In that case, it can be shown that
the age of the universe is given by
2
Age of universe = ----. (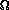 o = 1)
3 Ho
o = 1)
3 Ho
Multiply your previous result for the age of the universe by 2/3 to
calculate the revised age of the universe for the case when 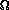 o = 1. Write your answer on your lab sheet
in Part IV, Section B:
o = 1. Write your answer on your lab sheet
in Part IV, Section B:
Age of universe = ________________ years. (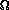 o = 1)
o = 1)
How does this compare to the presumed ages of the oldest globular
clusters? What can you infer about the actual value of 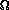 o by comparing the two ages you have
calculated? How does your evaluation of
o by comparing the two ages you have
calculated? How does your evaluation of 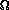 o compare to what you learned in class?
Write your answers on your lab sheet in the spaces provided.
o compare to what you learned in class?
Write your answers on your lab sheet in the spaces provided.
On to A note on scientific error
Back to Hubble's Law and the current Hubble
constant
Back to the table of contents
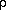 c, the universe will
continue to expand forever. It will get cold and dark. If the
density is higher than
c, the universe will
continue to expand forever. It will get cold and dark. If the
density is higher than 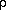 c
the gravitational attraction will eventually halt the expansion, then
begin a contraction toward what has been dubbed the "Big Crunch."
If
c
the gravitational attraction will eventually halt the expansion, then
begin a contraction toward what has been dubbed the "Big Crunch."
If 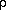 is just equal to
is just equal to 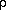 c the expansion will slow to a
stop, but only after an infinite amount of time has passed.
c the expansion will slow to a
stop, but only after an infinite amount of time has passed. 
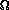 o, defined as
o, defined as 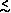 0.1). The other 90% is thought to be composed of
"exotic" particles we cannot easily detect.
0.1). The other 90% is thought to be composed of
"exotic" particles we cannot easily detect.