Measuring the Distance to Nearby Galaxies

This activity is originally from the Introductory Astronomy Clearinghouse,

created and maintained by the Astronomy Department at the University of Washington.

Procedure

Obtain a worksheet from your instructor.
From the Galaxy List, choose the first galaxy from the list on your worksheet.
Find the angular size of the galaxy using its image. The images used in this lab are negatives, so that bright objects -- such as stars and galaxies --appear dark. There may be more than one galaxy in the image; the galaxy of interest is always the one closest to the center. To measure the size, click on opposite ends of the galaxy, at either end of the longest diameter. Be sure to measure all the way to the faint outer edges. Otherwise, you may dramatically underestimate the size of the galaxy, and introduce a systematic error. The angular size of the galaxy (in milliradians; 1 mrad = 0.057 degrees = 206 arcseconds) will be displayed; record this number on your worksheet.
Repeat step 2 for all 10 of the galaxies on the worksheet.
As stated in the Background and Theory section, we assume that all of these galaxies are about the same size. From other methods we know that galaxies of the type used in this lab are about 22 kpc (1 kpc = 1000 pc) across. Find the distance to each galaxy using the small angle formula, adapted for the units we are using here:
d (Mpc) = s (kpc) / a (mrad),
and record this distance in your data table under Distance.
The full optical spectrum of the galaxy is shown at the top of the spectrum page. Below it are enlarged portions of the same spectrum, in the vicinity of some common spectral features. The small dark bar near the lower left corner of the sub-spectrum indicates the rest wavelength of the line.
1. Look for absorption lines of ionized calcium, lines designated by "H" and "K" [rest wavelengths of 3968.5 and 3933.7 Angstroms] and the emission of the H-alpha line of hydrogen [rest wavelength of 6562.8 Angstroms]. Remember: these spectra are of galaxies that are moving away from us and so the lines are going to be redshifted (shifted towards longer wavelengths); some, you will find out, by a large amount.
2. Spectra from spiral galaxies tend to be dominated by strong hydrogen emission lines along with some absorption lines. This is because spirals have plenty of gas in the disk which is being heated by newly formed stars. However, some spectra from the relatively gas-poor elliptical galaxies tend to show only absorption lines, or absorption lines with very weak hydrogen emission lines.
3. Not all of the dips and peaks come from the light of the galaxy. Each spectrum contains "noise" that is an unavoidable aspect of the data collection process. This noise makes it more difficult to accurately identify some of the spectral features, especially the absorption lines such as the pair due to calcium. Some of the spectra are much "noisier" than other spectra. Spectra with strong hydrogen emission lines will tend to have the "relative intensity" axis rescaled such that the "noise" artificially appears to be minimal.
Measure the wavelength by clicking at the middle of the spectral line in the galaxy's spectrum. For help getting started with the analysis of the spectra, click on this link to see an example using the data for NGC 1357. For this lab, you are to measure the red-shifted wavelength for Ca K, Ca H and H-alpha lines for each galaxy assigned to you.
Repeat step 4 for all 10 of the galaxies on the worksheet.
Calculate the redshift, z for each of the lines, and enter these data in the z boxes on the worksheet.
Find the average of the redshifts for each galaxy, and enter it in the table.
Use this average redshift to find the velocity: v = c z, where c represents the speed of light,
and enter this in the table under Velocity.
Make a graph of your data (please print out and use the graph paper provided), with distance on the x-axis, and velocity on the y-axis. Draw a straight line that best fits the points on the graph. Label the best fit line. On the worksheet, clearly and concisely explain why this this line must pass through the origin (the 0,0 point).
Measure the slope of this best-fit-line, where slope = rise / run. The slope of the line is the Hubble constant, in the funny units of km/sec/Mpc.
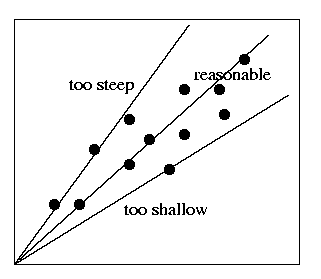
Your graph probably does not make a perfect line, and you will notice that you had to make a guess as to where to draw your line. Your line would have obviously been too steep if it had been drawn so it went steeper than the data points plotted the most to the high left. YOur line would have obviously been too shallow if it had been drawn so it went more shallow that the data points polotted the most to the low right. The only reasonable zone would have been somewhere inbetween. Estimate the uncertainty in the value of Ho by drawing the steepest reasonable line and the shallowest reasonable line on the graph. Label the steepest reasonable line and the shallowest reasonable line. Half of the difference between these two slopes is your uncertainty in H_o.
And now for the age of the universe!
If the universe has been expanding at a constant speed since its beginning, the universe's age would simply be 1/H_o. Convert H_o to inverse-seconds (1/sec) by cancelling out the distance units: 1 Mpc = 3.09 x 10¹⁹ km. The "expansion age" of the universe is t = 1/H_o, first in units of seconds and then as years.
How does this value compare to the age of the Sun? How does it compare to the ages of the oldest globular clusters?
Gravity will slow the expansion of the universe as the matter (bright matter and dark matter) that makes up the universe create an attractive force and tries to pull itself together. Thus, the Hubble constant has almost certainly not been constant over the lifetime of the universe. In the last decade astronomers have been surprised to learn that, in addition to gravity slowing down the expansion of the universe, there is another force (given the name "dark energy") that works to expand the universe beyond the push it was given by the initial force of the Big Bang. Clearly and concisely explain why the age of the universe you calculated above would compare to the actual age for a universe with a substantial contribution from dark energy.