Edwin Hubble, redshifted spectra, and distances to galaxies

During the 1920's, Edwin Powell Hubble demonstrated that the small hazy patches of light which were then known as "spiral nebulae" are actually entire galaxies containing hundreds of billions of stars.
Utilizing the 100-inch telescope at California's Mount Wilson Observatory (at the time the world's largest telescope) Hubble obtained spectra and measurements of the distance to a few dozen galaxies, leading to the discovery that the Universe is expanding. Hubble compared recession velocities of galaxies measured from their spectra to their apparent brightness estimated from photographic plates. In 1929 Hubble published his findings, detailing revealed that the fainter and smaller a galaxy appeared, the higher was its redshift.
Redshift is a term used to describe situations when an astronomical object is observed to being moving away from the observer, such that emission or absorption features in the object's spectum are observed to have shifted toward longer (red) wavelengths. The change in wavelength of the spectral features is due to the Doppler effect, the change in wavelength that results when a given object and an observer are in motion either toward or away from each other. The radiation coming from a moving object is shifted in wavelength:
where "lambda_0" is the rest wavelength of the radiation, and is "lambda_v" is the observed wavelength which has been shifted due to the radial motion between the object and the observer. It is common to use "delta_lambda" to represent the observed wavelength minus the rest wavelength. Wavelengths of optical light are usually measured in either Angstroms (1 Å = 10-10 m) or nanometers (1 nm = 10 -9 m).
In the data collected by Hubble, the characteristic absorption and emission line features in the spectrum due to hydrogen, calcium and other elements which appear at longer (redder) wavelengths than in a terrestrial laboratory. One can use the measured wavelengths of known spectral lines to determine the velocity of a galaxy. For example:
Absorption lines of hydrogen, normally measured to be at 4861Å and 6563Å, are measured in the spectrum of a particular galaxy to be at 4923Å and 6647Å.
The speed of light, c, has a constant value of 300,000 km/sec.
Therefore this galaxy has a redshift of
z = [(4923 - 4861) / 4861] and z = [(6647 - 6563) / 6563]
z = [62 / 4861] and z = [84 / 6563]
z = 0.01275
and the is moving away from us with a velocity, v = c * z = 300,000 km/sec * 0.01275 = 3826 km/sec
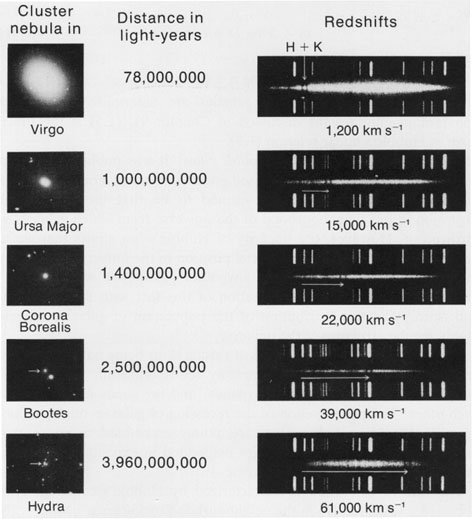
When Hubble plotted the redshift vs. the distance of the galaxies, he found a surprising relation: more distant galaxies are moving faster away from us. Hubble concluded that the fainter and smaller the galaxy, the more distant it is, and the faster it is moving away from us, or that the recessional velocity of a galaxy is proportional to its distance from us:
v = Ho d,
where v is the galaxy's velocity (in km/sec), d is the distance to the galaxy (in megaparsecs; 1 Mpc = 1 million parsecs), and Ho proportionality constant, called "The Hubble constant".
Hubble's Law states that the galaxy's recession speed = Ho * distance, where Ho is known as the Hubble constant and is a measure of the slope of the line through the distance versus recession velocity data. The line goes through the origin (0,0) because that represents our home position (zero distance) and we are not moving away from ourselves (zero speed).
To determine a galaxy's distance, we must rely on indirect methods. For instance, one assumption used by Hubble, and other early 20th century astronomers, is to assume all galaxies of the same type are the same physical size, no matter where they are. This is known as "the standard ruler" assumption. To determine the distance to a galaxy one would only need to measure its apparent (angular) size, and use the small angle equation: a = s / d, where a is the measured angular size (in radians!), s is the galaxy's true size (diameter), and d is the distance to the galaxy.
In order to precisely determine the value of Ho, we must determine the velocities and distances to many galaxies. Hubble's law has been confirmed by subsequent research and provides the cornerstone of modern relativistic cosmological theories of our expanding universe. In 1963 astronomers discovered cosmic objects known as quasars that exhibit larger redshifts than any of the remotest galaxies previously observed. The extremely large redshifts of various quasars suggest that they are moving away from the Earth at tremendous velocities (i.e., approximately 90 percent the speed of light) and thereby constitute some of the most distant objects in the universe.
Historical Note: It is not common for any other astronomers to be mentioned along with Edwin Hubble as being responsible for figuring out how the distance to a galaxy is related to its recession velocity. However, Hubble did not work alone and many other astronomers deserve credit for establishing the distance--redshift relationship.
Click below to begin the exercise: